El origen y la solución de las ecuaciones de segundo grado son de gran antigüedad. En Babilonia se conocieron algoritmospara resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso en el caso de que las dos soluciones sean positivas). La primera solución completa la desarrolló el matemático Al-Juarismi (o Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones.[cita requerida] Hay que esperar a Évariste Galois para conseguir resolver en general las ecuaciones polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una generalización de los métodos de resolución de las ecuaciones de segundo grado.
- La primera gran dificultad que surgió en la solución de ecuaciones cuadráticas se dio con la ecuación
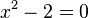en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1.No se podía expresar la raíz cuadrada de dos como razón de dos números enteros. 9 . Lo que permitió la formulación de números irracionales. - Luego , ya en el Renacimiento, al resolver
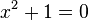, pues exige hallar un número real cuyo cuadrado sea -1; y se sabe que el cuadrado de cualquier real es positivo; lo que se superó con la adopción de números imaginarios y la definición de la unidad imaginaria i que cumple
No hay comentarios:
Publicar un comentario